Odolnosť dynamických systémov

Riešiteľka: Hana Krakovská

 

Stabilita patrí medzi najdôležitejšie pojmy v dynamických systémoch. Lokálna stabilita je klasický a dobre preštudovaný koncept, zatiaľ čo definícia a určenie „globálnej“ stability (odolnosti) nelineárneho systému je pomerne náročné. Za posledných niekoľko desaťročí sa na riešenie tohto problému vyvinulo mnoho rôznych postupov, ktoré boli primárne motivované aplikovanými problémami. Pojem odolnosti (resilience) má ale v súčasnosti množstvo navzájom nekonzistentných definícií. Práca [1] preto prináša rozsiahly, systematický prehľad ukazovateľov odolnosti v kontexte spojitých dynamických systémov, ako aj ich zovšeobecnenie a kategorizáciu podľa matematických vlastností. Tieto kroky sú dôležité na zabezpečenie spoľahlivejšieho, kvantitatívne porovnateľného a reprodukovateľného výskumu odolnosti v dynamických systémoch. Uvedené indikátory sú v práci porovnané aj v rámci klasického modelu z populačnej dynamiky.

Práca vznikla ako pokračovanie spolupráce na diplomovom projekte Hany Krakovskej so školiteľmi Christianom Kuehnom a Iacopo P. Longom z Fakulty matematiky Technickej univerzity Mníchov.

Publikácia viedla tento rok aj k dvom pozvaným prednáškam [2], [3].

 

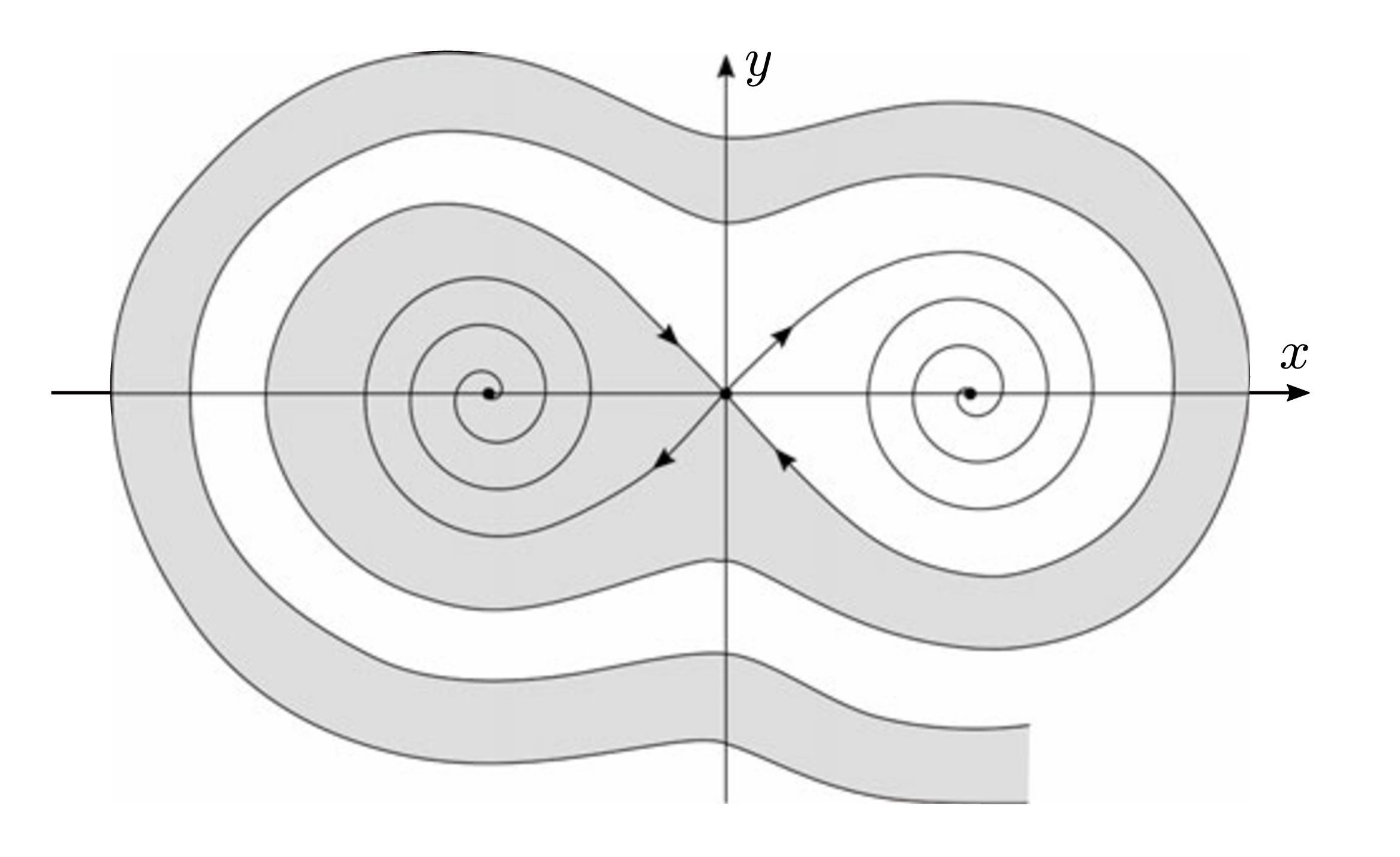
Obr.: Jednoduchý príklad výsledku analýzy stability. Nebudený Duffingov oscilátor predstavuje systém s tromi ekvilibriami, sedlovým bodom a dvomi pevnými bodmi. Pevné body sú asymptoticky stabilné a hranica oblasti príťažlivosti každého z nich je určená stabilnou varietou sedlového bodu.

 

Zahraničný partner

  • Fakulta matematiky Technickej univerzity Mníchov

Súvisiace projekty

  • VEGA č. 2/0023/22

Súvisiace publikácie a pozvané prednášky

  • KRAKOVSKÁ, Hana – KUEHN, C. – LONGO, I.P. Resilience of dynamical systems. In European Journal of Applied Mathematics, 2024, vol. 35, no. 1, p. 155-200. (2023: 2.3 – IF, Q1 – JCR, 0.845 – SJR, Q2 – SJR). ISSN 0956-7925. Dostupné na: https://doi.org/10.1017/S0956792523000141 (VEGA č. 2/0023/22: Causal analysis of measured signals and time series) Typ: ADMA
  • KRAKOVSKÁ, Hana. Resilience Indicators in Dynamical Systems. Lecture, invited by George Datseris (University of Exeter), Minisymposium on Multistability and global stability analysis, Conference Dynamics Days Europe, Bremen, July 29 – August 2, 2024
  • KRAKOVSKÁ, Hana. Resilience of attractors in dynamical systems. Lecture, invited by Pavol Bokes (FMFI UK, Bratislava), Seminar on the Qualitative Theory of Differential Equations, October 24, 2024