Development and testing of methods of causal analysis of measured time series and paradoxical results in applications
(Investigators: A. Krakovská, M. Chvosteková, J. Jakubík)
Causal analysis of large volumes of measured data is becoming a hot topic of research. Existing techniques have been shown to be insufficient and their non-critical use often leads to completely incorrect conclusions.
We have been working intensively on this topic for several years. We test existing methods and design our own solutions. In an extensive comparative study, we have shown that the classical Granger causality test should be used only in cases that allow autoregressive modeling. Newly-designed methods are more effective in complicated cases, such as the connection between complex nonlinear systems or apparent causality due to external influences [1].
However, none of the methods has been shown to be unreservedly applicable when the causal effect is significantly delayed. For the tested interconnected chaotic systems, the most suitable method is the evaluation of mutual information, while for discrete systems, the methods in reconstructed spaces succeeded better, including the method proposed by us [4]. However, if the dynamics of the studied systems contained a strong oscillating component, then all methods failed. We have therefore published a study in which we point out that the detection of delayed causality is one of the serious unresolved problems [3].
Another important paradox that we have pointed out concerns the rule that cause always precedes consequence. This time sequence is the first principle in defining causality. If we turn a measured time series over time, we expect mathematical methods of causality detection to switch cause and effect. This indeed happens with commonly investigated linear systems, but not with computer-generated chaotic systems.
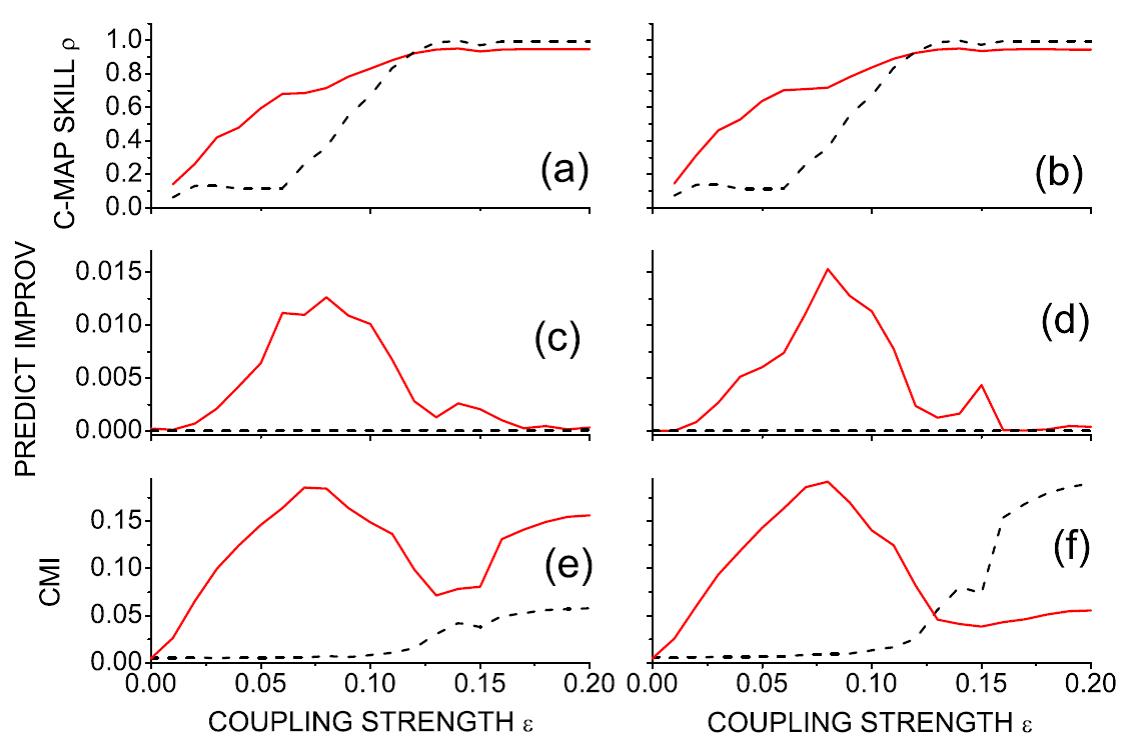
This surprising fact can have interesting consequences. For example, imagine that – as in the following figure – in the causal analysis, we turn the measured data in time and the cause does not exchange the task with the consequence.
One of the real examples in which we encounter this paradox is the analysis of how the rhythm of breathing affects the rhythm of the heart. Can our observation be a signal that the data being studied comes from a chaotic process? This would support some earlier research that looked at cardio-respiratory bonds in the context of the interaction of nonlinear, potentially chaotic oscillators.
The paradox regarding the flow of time in causally interconnected dynamic systems cannot yet be satisfactorily explained. But the severity of the problem is enormous. As we emphasized in a study prepared with colleagues from the Institute of Informatics of the Academy of Sciences of the Czech Republic, in many respects we are faced with the challenge of re-evaluating the current technique of causal analysis [2].
Fig. 1: Causality detection for two chaotic Rössler systems X and Y, connected unidirectionally with a bond strength from 0 to 0.2. Figures (a), (c) and (e) show the results of the three different causal methods tested in Article [2]. The actual direction of the causal connection X → Y corresponds to the red line, the opposite (unconnected) direction is the black dashed line. Paradoxically, if we turn the rows over time (Fig. (B), (d), (f)), causal methods repeat previous results, although we would expect them to switch cause and effect. If X and Y were defined as linearly interconnected autoregressive processes, we would not observe this paradox.
Related projects:
- VEGA 2/0011/16
- MAD – Bilaterálny mobilitný projekt, SAV-AV ČR 15-18
- APVV – 15-0295
Publications:
- KRAKOVSKÁ, A. – JAKUBÍK, J. – CHVOSTEKOVÁ, M. – COUFAL, D. – JAJCAY, N. – PALUŠ, M. Comparison of six methods for the detection of causality in a bivariate time series. In Physical Review E, 2018, vol. 97, p. 042207. ISSN 2470-0045. (2.284-IF2017)
- PALUŠ, M. – KRAKOVSKÁ, A. – JAKUBÍK, J. – CHVOSTEKOVÁ, M. Causality, dynamical systems and the arrow of time. In Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018, vol. 28, no. 7, p. 075307. ISSN 1054-1500. (2.415-IF2017)
- COUFAL, D. – JAKUBÍK, J. – JAJCAY, N. – HLINKA, J. – KRAKOVSKÁ, A. – PALUŠ, M. Detection of coupling delay: A problem not yet solved. In Chaos, 2017, vol. 27, no. 8, p. 083109. ISSN 1054-1500. (2.283-IF2016)
- KRAKOVSKÁ, A. – HANZELY, Filip. Testing for causality in reconstructed state spaces by an optimized mixed prediction method. In Physical Review E, 2016, vol. 94, no. 5, p. 052203. ISSN 2470-0045. (2.252-IF2015).
 Contacts
Contacts Intranet
Intranet SK
SK